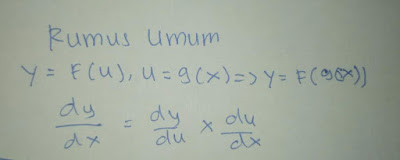GRAFIK TURUNAN LANJUTAN

 1. TURUNKAN PERSAMAAN

2. TURUNKAN PERSAMAAN PERTAMA MENJADI TURUNAN KEDUA 

3. CARI TITIK KRITIS DARI TURUNAN

4. TENTUKAN INTERVAL FUNGSI NAIK / TURUN

5. TENTUKAN TITIK BELOK

6. TENTUKAN KECEKUNGAN GRAFIK

7. UJI NILAI EKSTRIM

8. BUAT GRAFIK

GRAFIK TURUNAN

Langkah langkah  dalam mengerjakan grafik turunan

1. Turunankan persamaan yang ada di soal

2. cari akar-akar dari persamaan yang telah diturunkan (pada soal ini saya menggunakan rumus abc untuk mencari akar-akarnya)

3. cari titik kritis dari turunan

4. Buat Interval fungsi naik turun dengan garis bilangan

5. gambar grafik turunan

6. buat kesimpulan

CARI TITIK KRITIS DARI TURUNAN 

BUAT INTERVAL FUNGSI NAIK TURUN DENGAN GARIS BILANGAN

GAMBAR GRAFIK TURUNAN

KESIMPULAN

LIMIT TAK TENTU (∞^0 ,0^0 ,1^∞)

LIMIT TAK TENTU

(∞^0  ,0^0  ,1^∞)

Contoh :

LIMIT TAK TENTU(0/0 , ∞/∞ , 0 . ∞ , ∞ - ∞ )

Ada beberapa bentuk limit tak tentu, yuk simak!

1. Untuk 0/0

2. Untuk  ∞/∞ 

3. Untuk 0 . ∞ 

4. Untuk ∞ - ∞ 

TURUNAN IMPLISIT , TURUNAN KEDUA , FUNGSI EKSPONEN ASLI

Fungsi implisit adalah fungsi yang terdiri dari dua atau lebih variabel yakni variabel bebas dan variabel tak bebas, yang berada dalam satu ruas dan tidak bisa dipisahkan pada ruas yang berbeda.

Menurunkan fungsi implisit, tak jauh beda dengan menurunkan fungsi variabel tunggal, yakni dengan menggunakan notasi Leibniz (dy/dx). Berikut ini, hal yang harus dipahami dalam menurunkan fungsi implisit khususnya yang memiliki dua variabel (x dan y).

CONTOH SOAL

TURUNAN KEDUA

FUNGSI EKSPONEN ASLI

CONTOH SOAL

GRAFIK TURUNAN LANJUTAN

Turunan Fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalkan fungsi f menjadi f’ yang memiliki nilai tidak beraturan.

CONTOH SOAL

ATURAN TURUNAN FUNGSI

CONTOH SOAL

ATURAN RANTAI adalah aturan rantai adalah rumus untuk turunan fungsi komposit (fungsi bersusun) dari dua fungsi matematiks

 TURUNAN TRIGONOMETRI

CONTOH SOAL

LIMIT FUNGSI TRIGONOMETRI

Limit trigonometri adalah nilai terdekat suatu sudut pada fungsi trigonometri. Perhitungan limit fungsi trigonometri bisa langsung disubtitusikan seperti limit fungsi aljabar tetapi ada fungsi trigonometri yang harus diubah terlebih dahulu ke identitas trigonometri untuk limit tak tentu yaitu limit yang apabila kita langsung subtitusikan nilai nya bernilai 0, atau bisa juga untuk limit tak tentu tidak harus memakai identitas tetapi memakai teorema limit trigonometri dan ada juga yang memakai identitas dan teorema. Jadi, apabila suatu fungsi limit trigonometri di subtitusikan nilai yang paling mendekati nya menghasilkan dan maka kita harus menyelesaikan dengan cara lain.

CONTOH SOAL

KONTINUITAS

CONTOH SOAL